A Sphere and a Cone, Oh My!
Challenge Problem #15
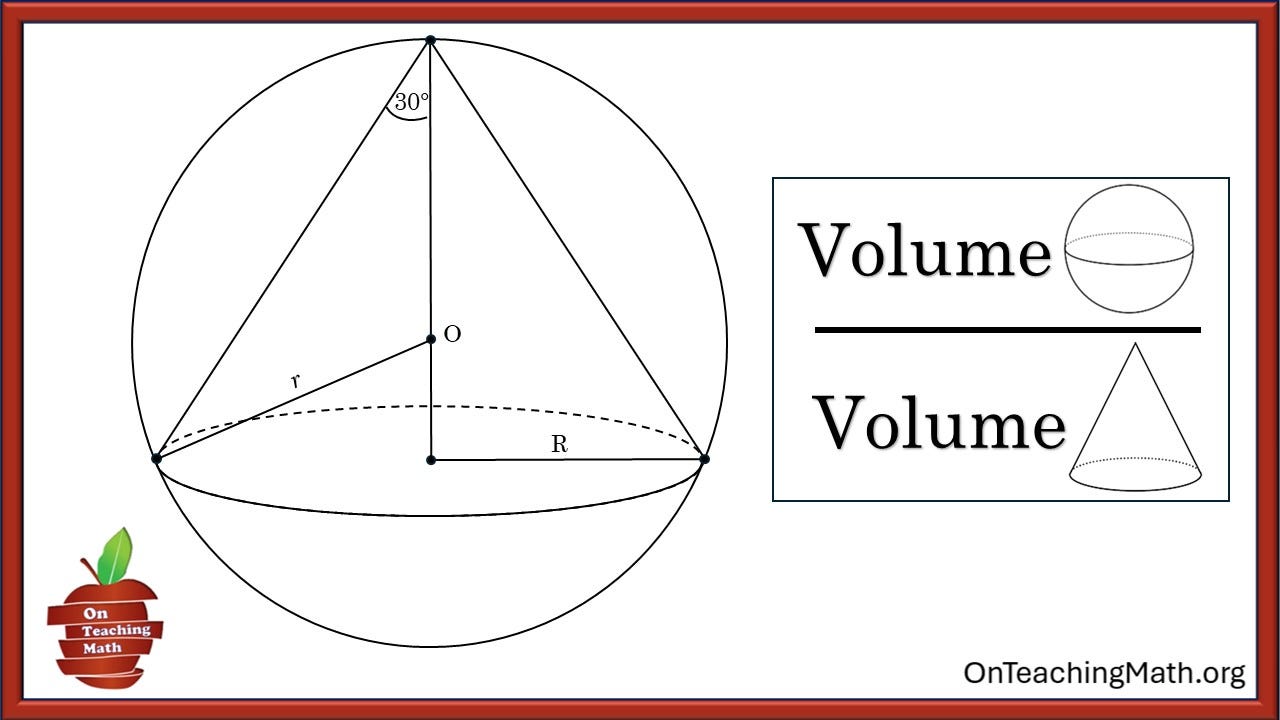
Here are the details: There is a sphere, radius r. Inscribed in the sphere is a right-angled cone, radius R.
Our job is to find the ratio of the volumes, sphere: cone.
As is always the case, I will pause here and allow you some time to ponder, and try a few things. The level of perseverance is yours to choose. Below you will find a series of three clues of increasing strength, and then the solution. (Increasing strength means that each clue reveals a larger chunk of information required to answer the problem than the previous clue revealed.)
Clues
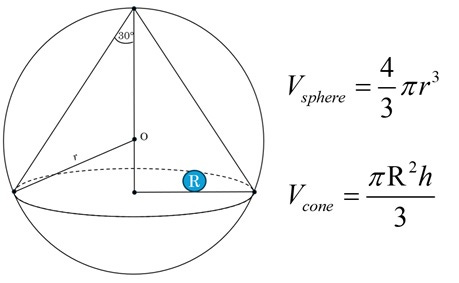
Clue #1: You need two formulas. When writing these out you’ll likely realize a substitution is required. Is the radius from the cone the same as the radius of the sphere?
Clue #2: What about the height of the cone? Can you write an expression for the height of the cone in terms of R? Did you see that a special right triangle is lying in wait for you there?
Clue #3: Point O to the top of the cone is the radius of the sphere. The base of the cone to the edge of the sphere is R. So, from the base of the cone to the sphere’s center is R – r. Use the Pythagorean Theorem to rewrite r in terms of R.
Solution
Video
Let’s begin with formulas because they give us a place to start, a first step. Since the problem has labeled the radius of the cone R, let’s start using that instead of r, since each radius is different.
In the cone’s formula, we have two variables. There is another variable in the formula for the sphere. Since our goal is to write a ratio, that presumably simplifies nicely, we will need to rewrite the variables into a single variable. We will do this by relating them to each other.
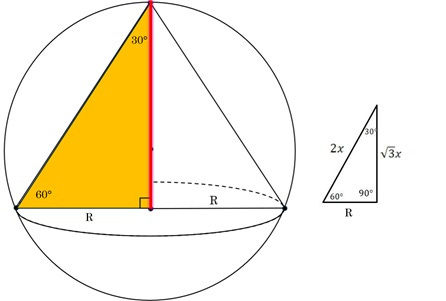
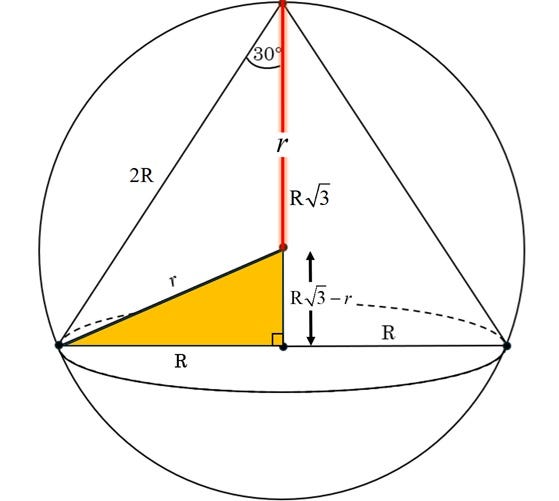
For example, our next step is going to be to rewrite the height of the cone in terms of the radius (R) of the cone. Since the cone is a right cone and an angle at the top marked 30°, we know we have a 30°- 60°- 90° right triangle.
In such a triangle, the long leg’s distance is the distance of the short leg times the square root of three. Since the short leg is the radius of the cone, R, the long leg, which is the height of the cone, is R times the square root of three.
Let’s now turn our attention to the sphere. If we can rewrite r (the sphere’s radius) in terms of R (the cone’s radius), we are done.
We know that the height of the cone is R times “root three.” We also know that point O, which lies on the cone’s height, is the center of the circle, making the distance from O to the top of the cone the sphere’s radius, r.
Since the entire distance is “R root three,” and part of it is r, the remaining bottom part is the difference of the two, “R root three” minus r.
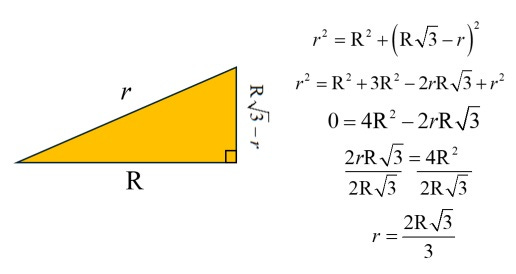
What’s more, is that there is a beautiful little right triangle ready for us to explore. We know the radius is r, the long leg is R, and the short leg is “R root three” – r. Time for some more Pythagorean Theorem!
If you are careful with squaring and combining like terms, the algebraic steps shown here are much easier than they appear. In the end you will rationalize the denominator to clean up the “root three,” but that’s it!
Now we know what r is in terms of R.
We can plug this back into our original equation to get the following.
From here there are no mysteries. While it is easy to make computational errors, and for those that aren’t up to date on their algebraic skills this can be tricky, but there aren’t any substitutions or hidden relationships remaining to uncover. To arrive at the final answer we just simplify the numerator, then multiply by the reciprocal of the denominator. The expression cleans up very nicely.
If you want to see the simplification you can see it in a YouTube video I made of this problem. But for now, I’ll leave you with the final answer.
Wrap-Up
This is a fantastic problem. I post a problem like this every week in my classroom for anyone who might be interested. This one proved a bit daunting for most, but I still had a few juniors willing to tackle it.
If you’re a math teacher and would like to use this problem in your classroom I would be happy to share with you a PowerPoint, handout, and Google Forms quiz. You can find them all on my website, linked here. I really would like to encourage you to just post a problem a week and see what happens. Discuss it, and encourage them, but don’t entice them with extra credit or anything like that.
The idea here is that school, like work, can really suck the fun out of things. Math can be a lot of fun, it’s a puzzle. These problems are used in such a spirit.


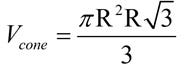
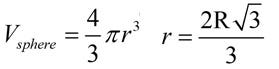
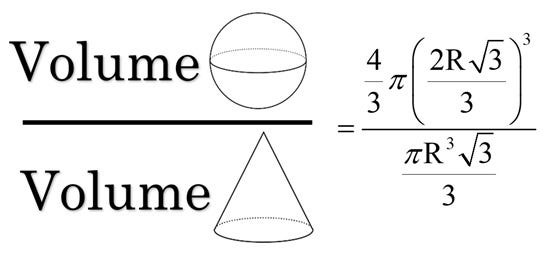
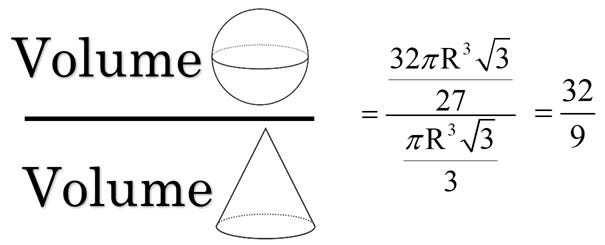
Good problem. I assumed r = 1, and used that to find the side length of the cone, sqrt 3, using law of cosines. The R = sqrt 3 / 2, h = 1.5, and I was all set to solve the problem.